Tuning inner kernel parameters of SMC#
import jax
from jax import numpy as jnp
import arviz as az
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import functools
from datetime import date
rng_key = jax.random.key(int(date.today().strftime("%Y%m%d")))
This notebook is a continuation of Use Tempered SMC to Improve Exploration of MCMC Methods.
In that notebook, we tried sampling from a multimodal distribution using HMC, NUTS
and SMC with an HMC kernel. Only the latter was able to get samples from both modes of the distribution.
Recall that when setting the HMC parameters
hmc_parameters = dict(
step_size=1e-4, inverse_mass_matrix=inv_mass_matrix, num_integration_steps=1
)
these were fixed across all iterations of SMC. The efficiency of an SMC sampler can be improved by informing the inner kernel parameters using the particles population. We can tune one or many inner kernel parameters before mutating the particles in step \(i\), using the particles outputted by step \(i-1\). This notebook illustrates such tuning using IRMH (Independent Rosenbluth Metropolis-Hastings) with a multivariate normal proposal distribution.
See Design choice (c) of section 2.1.3 from https://arxiv.org/abs/1808.07730.
n_particles = 5000
from jax.scipy.stats import multivariate_normal
def V(x):
return 5 * jnp.sum(jnp.square(x**2 - 1))
def prior_log_prob(x):
d = x.shape[0]
return multivariate_normal.logpdf(x, jnp.zeros((d,)), jnp.eye(d))
loglikelihood = lambda x: -V(x)
def density():
linspace = jnp.linspace(-2, 2, 5000).reshape(-1, 1)
lambdas = jnp.linspace(0.0, 1.0, 5)
prior_logvals = jnp.vectorize(prior_log_prob, signature="(d)->()")(linspace)
potential_vals = jnp.vectorize(V, signature="(d)->()")(linspace)
log_res = prior_logvals.reshape(1, -1) - jnp.expand_dims(
lambdas, 1
) * potential_vals.reshape(1, -1)
density = jnp.exp(log_res)
normalizing_factor = jnp.sum(density, axis=1, keepdims=True) * (
linspace[1] - linspace[0]
)
density /= normalizing_factor
return density
def initial_particles_multivariate_normal(dimensions, key, n_samples):
return jax.random.multivariate_normal(
key, jnp.zeros(dimensions), jnp.eye(dimensions) * 2, (n_samples,)
)
IRMH without tuning#
The proposal distribution is normal with fixed parameters across all iterations.
from blackjax import adaptive_tempered_smc
from blackjax.smc import resampling as resampling, solver, extend_params
from blackjax import irmh
def irmh_experiment(dimensions, target_ess, num_mcmc_steps):
mean = jnp.zeros(dimensions)
cov = jnp.diag(jnp.ones(dimensions)) * 2
def irmh_proposal_distribution(rng_key):
return jax.random.multivariate_normal(rng_key, mean, cov)
def proposal_logdensity_fn(proposal, state):
return jnp.log(
jax.scipy.stats.multivariate_normal.pdf(state.position, mean=mean, cov=cov)
)
def step(key, state, logdensity):
return irmh(logdensity, irmh_proposal_distribution,proposal_logdensity_fn).step(key, state)
fixed_proposal_kernel = adaptive_tempered_smc(
prior_log_prob,
loglikelihood,
step,
irmh.init,
mcmc_parameters={},
resampling_fn=resampling.systematic,
target_ess=target_ess,
root_solver=solver.dichotomy,
num_mcmc_steps=num_mcmc_steps,
)
def inference_loop(kernel, rng_key, initial_state):
def cond(carry):
_, state, *_ = carry
return state.tempering_param < 1
def body(carry):
i, state, op_key, curr_loglikelihood = carry
op_key, subkey = jax.random.split(op_key, 2)
state, info = kernel(subkey, state)
return (
i + 1,
state,
op_key,
curr_loglikelihood + info.log_likelihood_increment,
)
total_iter, final_state, _, log_likelihood = jax.lax.while_loop(
cond, body, (0, initial_state, rng_key, 0.0)
)
return total_iter, final_state.particles
return fixed_proposal_kernel, inference_loop
IRMH tuning the diagonal of the covariance matrix#
Although the proposal distribution is always normal, the mean and diagonal of the covariance matrix are fitted from the particles outcome of the \(i-th\) step, in order to mutate them in the step \(i+1\)
from blackjax.smc.inner_kernel_tuning import as_top_level_api as inner_kernel_tuning
from blackjax.smc.tuning.from_particles import (
particles_covariance_matrix,
particles_stds,
particles_means,
)
def tuned_irmh_loop(kernel, rng_key, initial_state):
def cond(carry):
_, state, *_ = carry
return state.sampler_state.tempering_param < 1
def body(carry):
i, state, op_key = carry
op_key, subkey = jax.random.split(op_key, 2)
state, info = kernel(subkey, state)
return i + 1, state, op_key
def f(initial_state, key):
total_iter, final_state, _ = jax.lax.while_loop(
cond, body, (0, initial_state, key)
)
return total_iter, final_state
total_iter, final_state = f(initial_state, rng_key)
return total_iter, final_state.sampler_state.particles
def tuned_irmh_experiment(dimensions, target_ess, num_mcmc_steps):
kernel = irmh.build_kernel()
def step_fn(key, state, logdensity, means, stds):
cov = jnp.square(jnp.diag(stds))
proposal_distribution = lambda key: jax.random.multivariate_normal(
key, means, cov
)
def proposal_logdensity_fn(proposal, state):
return jnp.log(
jax.scipy.stats.multivariate_normal.pdf(
state.position, mean=means, cov=cov
)
)
return kernel(key, state, logdensity, proposal_distribution, proposal_logdensity_fn)
kernel_tuned_proposal = inner_kernel_tuning(
logprior_fn=prior_log_prob,
loglikelihood_fn=loglikelihood,
mcmc_step_fn=step_fn,
mcmc_init_fn=irmh.init,
resampling_fn=resampling.systematic,
smc_algorithm=adaptive_tempered_smc,
mcmc_parameter_update_fn=lambda _, state, info: extend_params(
{"means":particles_means(state.particles), "stds":particles_stds(state.particles)}),
initial_parameter_value=extend_params(
{"means":jnp.zeros(dimensions), "stds":jnp.ones(dimensions) * 2}),
target_ess=target_ess,
num_mcmc_steps=num_mcmc_steps,
)
return kernel_tuned_proposal, tuned_irmh_loop
IRMH tuning the covariance matrix.#
In this case not only the diagonal but all elements of the covariance matrix are fitted based on the outcome particles.
def irmh_full_cov_experiment(dimensions, target_ess, num_mcmc_steps):
kernel = irmh.build_kernel()
def step(key, state, logdensity, means, cov):
"We need step to be vmappable over the parameter space, so we wrap it to make all parameter Jax Arrays or JaxTrees"
proposal_distribution = lambda key: jax.random.multivariate_normal(
key, means, cov
)
def proposal_logdensity_fn(proposal, state):
return jnp.log(
jax.scipy.stats.multivariate_normal.pdf(
state.position, mean=means, cov=cov
)
)
return kernel(key, state, logdensity, proposal_distribution, proposal_logdensity_fn)
def mcmc_parameter_update_fn(_, state, info):
covariance = jnp.atleast_2d(particles_covariance_matrix(state.particles))
return extend_params({"means":particles_means(state.particles), "cov":covariance})
kernel_tuned_proposal = inner_kernel_tuning(
logprior_fn=prior_log_prob,
loglikelihood_fn=loglikelihood,
mcmc_step_fn=step,
mcmc_init_fn=irmh.init,
resampling_fn=resampling.systematic,
smc_algorithm=adaptive_tempered_smc,
mcmc_parameter_update_fn=mcmc_parameter_update_fn,
initial_parameter_value=extend_params({"means":jnp.zeros(dimensions), "cov":jnp.eye(dimensions) * 2}),
target_ess=target_ess,
num_mcmc_steps=num_mcmc_steps,
)
return kernel_tuned_proposal, tuned_irmh_loop
def smc_run_experiment(runnable, target_ess, num_mcmc_steps, dimen, key=rng_key):
key, initial_particles_key, iterations_key = jax.random.split(key, 3)
initial_particles = initial_particles_multivariate_normal(
dimen, initial_particles_key, n_particles
)
kernel, inference_loop = runnable(dimen, target_ess, num_mcmc_steps)
_, particles = inference_loop(
kernel.step, iterations_key, kernel.init(initial_particles)
)
return particles
dimensions_to_try = [10, 20, 30]
experiments = []
dimensions = []
particles = []
for dims in dimensions_to_try:
for exp_id, experiment in (
("irmh", irmh_experiment),
("tune_diag", tuned_irmh_experiment),
("tune_full_cov", irmh_full_cov_experiment),
):
experiment_particles = smc_run_experiment(experiment, 0.5, 20, dims)
experiments.append(exp_id)
dimensions.append(dims)
particles.append(experiment_particles)
results = pd.DataFrame(
{"experiment": experiments, "dimensions": dimensions, "particles": particles}
)
linspace = jnp.linspace(-2, 2, 5000).reshape(-1, 1).squeeze()
def plot(post, sampler, dimensions, ax):
post = np.asarray(post)
dimensions = post.shape[1]
for dim in range(dimensions):
az.plot_kde(post[:, dim], ax=ax)
_ = ax.plot(linspace, density()[-1], c="red")
rows = len(dimensions_to_try)
cols = 3
samplers = ["irmh", "tune_diag", "tune_full_cov"]
fig, axs = plt.subplots(rows, cols, figsize=(cols * 10, rows * 5))
plt.rcParams.update({"font.size": 22})
for ax, lab in zip(axs[:, 0], dimensions_to_try):
ax.set(ylabel=f"Dimensions = {lab}")
for ax, lab in zip(axs[0, :], samplers):
ax.set(title=lab)
for col, experiment in enumerate(samplers):
for row, dimension in enumerate(dimensions_to_try):
particles = (
results[
(results.experiment == experiment) & (results.dimensions == dimension)
]
.iloc[0]
.particles
)
plot(particles, experiment, dimension, axs[row, col])
fig.tight_layout()
fig.suptitle(
"""Sampler comparison for increasing number of posterior dimensions.
Each plot displays all dimensions from the posterior, overlayed. The red curve is the actual marginal distribution."""
)
plt.show()
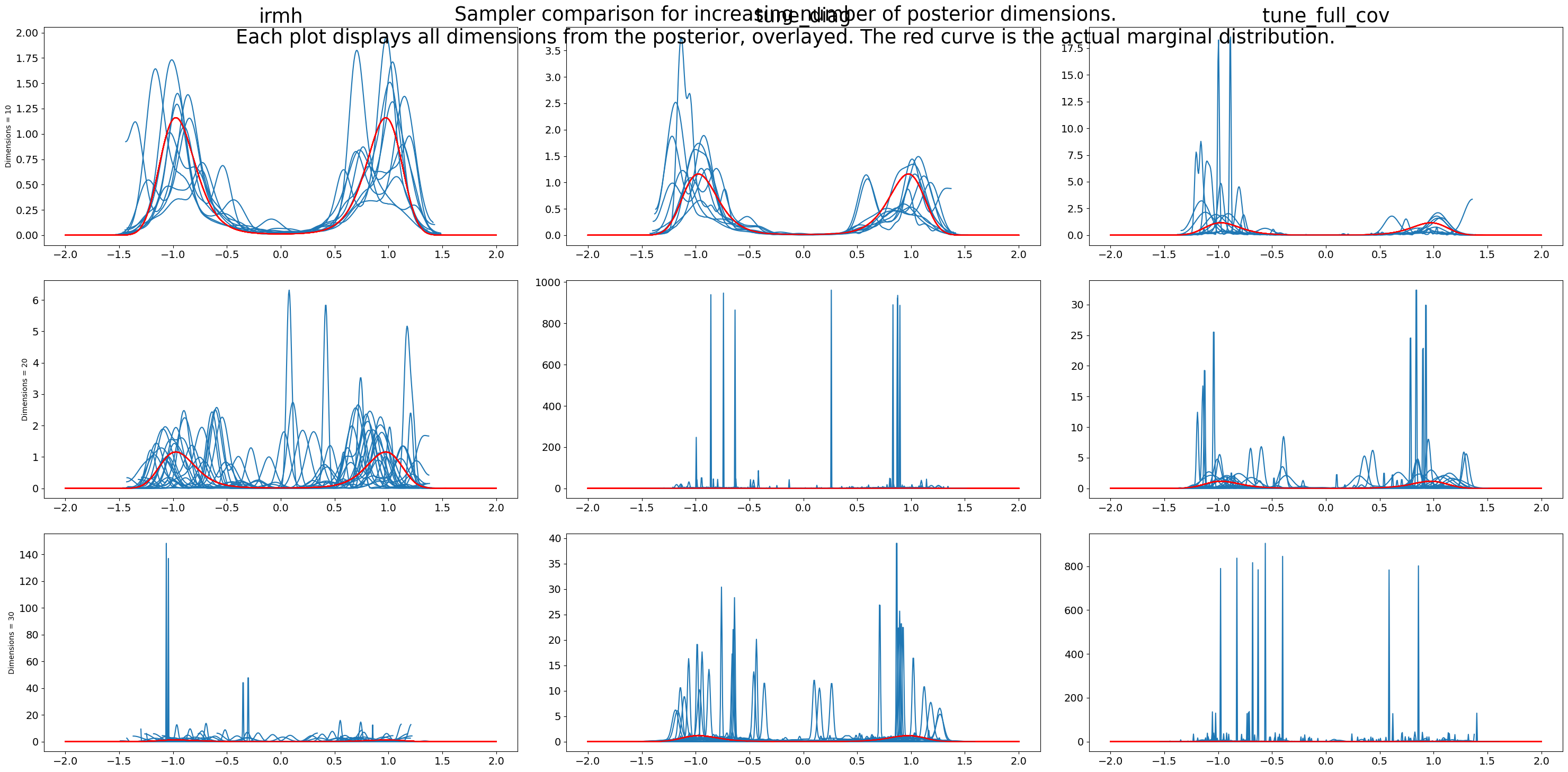
As seen in the previous figure, as dimensions increase, performance degrades. More tuning, less performance degradation.