Change of Variable in HMC

Change of Variable in HMC#

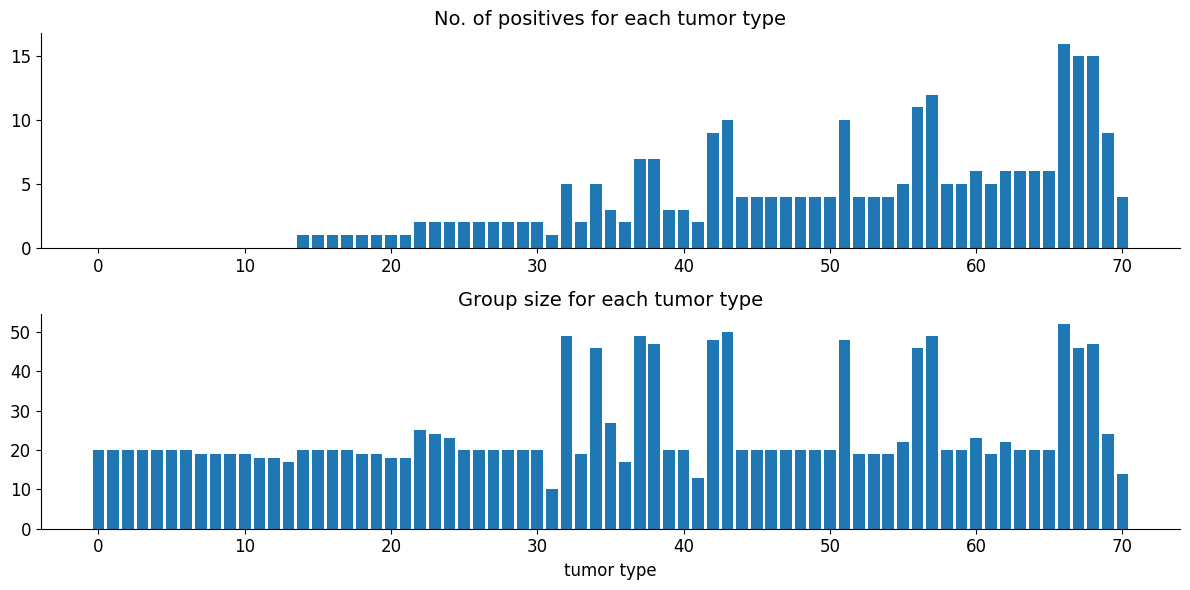
Rat tumor problem: We have J certain kinds of rat tumor diseases. For each kind of tumor, we test \(N_{j}\) people/animals and among those \(y_{j}\) tested positive. Here we assume that \(y_{j}\) is distrubuted with Binom(\(N_{i}\), \(\theta_{i}\)). Our objective is to approximate \(\theta_{j}\) for each type of tumor.

In particular we use following binomial hierarchical model where \(y_{j}\) and \(N_{j}\) are observed variables.

\[\begin{split}\begin{align} y_{j} &\sim \text{Binom}(N_{j}, \theta_{j}) \label{eq:1} \\ \theta_{j} &\sim \text{Beta}(a, b) \label{eq:2} \\ p(a, b) &\propto (a+b)^{-5/2} \end{align}\end{split}\]
Hide code cell content 
import matplotlib.pyplot as plt

plt.rcParams["axes.spines.right"] = False
plt.rcParams["axes.spines.top"] = False
plt.rcParams["xtick.labelsize"] = 12
plt.rcParams["ytick.labelsize"] = 12

import pandas as pd

pd.set_option("display.max_rows", 80)

import jax

from datetime import date
rng_key = jax.random.key(int(date.today().strftime("%Y%m%d")))
Hide code cell content 
import arviz as az
import jax.numpy as jnp

import blackjax
import tensorflow_probability.substrates.jax as tfp

tfd = tfp.distributions
tfb = tfp.bijectors
Hide code cell content 
# index of array is type of tumor and value shows number of total people tested.
group_size = jnp.array(
    [
        20,
        20,
        20,
        20,
        20,
        20,
        20,
        19,
        19,
        19,
        19,
        18,
        18,
        17,
        20,
        20,
        20,
        20,
        19,
        19,
        18,
        18,
        25,
        24,
        23,
        20,
        20,
        20,
        20,
        20,
        20,
        10,
        49,
        19,
        46,
        27,
        17,
        49,
        47,
        20,
        20,
        13,
        48,
        50,
        20,
        20,
        20,
        20,
        20,
        20,
        20,
        48,
        19,
        19,
        19,
        22,
        46,
        49,
        20,
        20,
        23,
        19,
        22,
        20,
        20,
        20,
        52,
        46,
        47,
        24,
        14,
    ],
    dtype=jnp.float32,
)

# index of array is type of tumor and value shows number of positve people.
n_of_positives = jnp.array(
    [
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        0,
        1,
        1,
        1,
        1,
        1,
        1,
        1,
        1,
        2,
        2,
        2,
        2,
        2,
        2,
        2,
        2,
        2,
        1,
        5,
        2,
        5,
        3,
        2,
        7,
        7,
        3,
        3,
        2,
        9,
        10,
        4,
        4,
        4,
        4,
        4,
        4,
        4,
        10,
        4,
        4,
        4,
        5,
        11,
        12,
        5,
        5,
        6,
        5,
        6,
        6,
        6,
        6,
        16,
        15,
        15,
        9,
        4,
    ],
    dtype=jnp.float32,
)

# number of different kind of rat tumors
n_rat_tumors = len(group_size)
Hide code cell source 
_, axes = plt.subplots(2, 1, figsize=(12, 6))
axes[0].bar(range(n_rat_tumors), n_of_positives)
axes[0].set_title("No. of positives for each tumor type", fontsize=14);
axes[1].bar(range(n_rat_tumors), group_size)
axes[1].set_xlabel("tumor type", fontsize=12)
axes[1].set_title("Group size for each tumor type", fontsize=14)
plt.tight_layout();
../_images/28eeb63cffff9411e6b79abb95f82e20176ed6f9b03659ccaf48920f3aef4900.png

Posterior Sampling#

Now we use Blackjax’s NUTS algorithm to get posterior samples of \(a\), \(b\), and \(\theta\)

from collections import namedtuple

params = namedtuple("model_params", ["a", "b", "thetas"])


def joint_logdensity(params):
    # improper prior for a,b
    logdensity_ab = jnp.log(jnp.power(params.a + params.b, -2.5))

    # logdensity prior of theta
    logdensity_thetas = tfd.Beta(params.a, params.b).log_prob(params.thetas).sum()

    # loglikelihood of y
    logdensity_y = jnp.sum(
        tfd.Binomial(group_size, probs=params.thetas).log_prob(n_of_positives)
    )

    return logdensity_ab + logdensity_thetas + logdensity_y

We take initial parameters from uniform distribution

rng_key, init_key = jax.random.split(rng_key)
n_params = n_rat_tumors + 2


def init_param_fn(seed):
    """
    initialize a, b & thetas
    """
    key1, key2, key3 = jax.random.split(seed, 3)
    return params(
        a=tfd.Uniform(0, 3).sample(seed=key1),
        b=tfd.Uniform(0, 3).sample(seed=key2),
        thetas=tfd.Uniform(0, 1).sample(n_rat_tumors, seed=key3),
    )


init_param = init_param_fn(init_key)
joint_logdensity(init_param)  # sanity check

Array(-1594.6903, dtype=float32)

Now we use blackjax’s window adaption algorithm to get NUTS kernel and initial states. Window adaption algorithm will automatically configure inverse_mass_matrix and step size

%%time
warmup = blackjax.window_adaptation(blackjax.nuts, joint_logdensity)

# we use 4 chains for sampling
n_chains = 4
rng_key, init_key, warmup_key = jax.random.split(rng_key, 3)
init_keys = jax.random.split(init_key, n_chains)
init_params = jax.vmap(init_param_fn)(init_keys)

@jax.vmap
def call_warmup(seed, param):
    (initial_states, tuned_params), _ = warmup.run(seed, param, 1000)
    return initial_states, tuned_params

warmup_keys = jax.random.split(warmup_key, n_chains)
initial_states, tuned_params = jax.jit(call_warmup)(warmup_keys, init_params)

CPU times: user 6.76 s, sys: 700 ms, total: 7.46 s
Wall time: 4.87 s

Now we write inference loop for multiple chains

def inference_loop_multiple_chains(
    rng_key, initial_states, tuned_params, log_prob_fn, num_samples, num_chains
):
    kernel = blackjax.nuts.build_kernel()

    def step_fn(key, state, **params):
        return kernel(key, state, log_prob_fn, **params)

    def one_step(states, rng_key):
        keys = jax.random.split(rng_key, num_chains)
        states, infos = jax.vmap(step_fn)(keys, states, **tuned_params)
        return states, (states, infos)

    keys = jax.random.split(rng_key, num_samples)
    _, (states, infos) = jax.lax.scan(one_step, initial_states, keys)

    return (states, infos)

%%time
n_samples = 1000
rng_key, sample_key = jax.random.split(rng_key)
states, infos = inference_loop_multiple_chains(
    sample_key, initial_states, tuned_params, joint_logdensity, n_samples, n_chains
)

CPU times: user 6.15 s, sys: 454 ms, total: 6.6 s
Wall time: 3.21 s

Arviz Plots#

We have all our posterior samples stored in states.position dictionary and infos store additional information like acceptance probability, divergence, etc. Now, we can use certain diagnostics to judge if our MCMC samples are converged on stationary distribution. Some of widely diagnostics are trace plots, potential scale reduction factor (R hat), divergences, etc. Arviz library provides quicker ways to anaylze these diagnostics. We can use arviz.summary() and arviz_plot_trace(), but these functions take specific format (arviz’s trace) as a input.

Hide code cell content 
def arviz_trace_from_states(states, info, burn_in=0):
    position = states.position
    if isinstance(position, jax.Array):  # if states.position is array of samples
        position = dict(samples=position)
    else:
        try:
            position = position._asdict()
        except AttributeError:
            pass

    samples = {}
    for param in position.keys():
        ndims = len(position[param].shape)
        if ndims >= 2:
            samples[param] = jnp.swapaxes(position[param], 0, 1)[
                :, burn_in:
            ]  # swap n_samples and n_chains
            divergence = jnp.swapaxes(info.is_divergent[burn_in:], 0, 1)

        if ndims == 1:
            divergence = info.is_divergent
            samples[param] = position[param]

    trace_posterior = az.convert_to_inference_data(samples)
    trace_sample_stats = az.convert_to_inference_data(
        {"diverging": divergence}, group="sample_stats"
    )
    trace = az.concat(trace_posterior, trace_sample_stats)
    return trace

# make arviz trace from states
trace = arviz_trace_from_states(states, infos)
summ_df = az.summary(trace)
summ_df
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
a 0.699 0.131 0.514 0.940 0.063 0.048 5.0 13.0 2.65
b 2.057 1.095 0.992 4.129 0.544 0.416 4.0 12.0 4.15
thetas[0] 0.054 0.050 0.000 0.139 0.023 0.017 6.0 38.0 1.83
thetas[1] 0.030 0.041 0.000 0.117 0.020 0.015 6.0 13.0 1.98
thetas[2] 0.020 0.017 0.000 0.046 0.007 0.005 7.0 81.0 1.60
thetas[3] 0.170 0.096 0.012 0.330 0.046 0.035 5.0 11.0 2.89
thetas[4] 0.017 0.020 0.000 0.061 0.007 0.005 7.0 32.0 1.52
thetas[5] 0.109 0.079 0.003 0.231 0.039 0.030 5.0 11.0 2.77
thetas[6] 0.021 0.021 0.000 0.059 0.008 0.006 7.0 11.0 1.54
thetas[7] 0.116 0.156 0.000 0.384 0.077 0.059 5.0 13.0 2.33
thetas[8] 0.126 0.133 0.000 0.361 0.066 0.050 5.0 18.0 2.47
thetas[9] 0.112 0.132 0.000 0.346 0.066 0.050 5.0 11.0 2.61
thetas[10] 0.121 0.163 0.002 0.407 0.081 0.062 5.0 15.0 2.46
thetas[11] 0.180 0.214 0.000 0.546 0.106 0.082 5.0 11.0 2.30
thetas[12] 0.026 0.018 0.000 0.054 0.008 0.006 6.0 48.0 1.73
thetas[13] 0.076 0.046 0.000 0.149 0.019 0.015 6.0 16.0 1.96
thetas[14] 0.102 0.102 0.018 0.286 0.051 0.039 5.0 11.0 2.35
thetas[15] 0.074 0.044 0.011 0.144 0.020 0.015 6.0 21.0 1.87
thetas[16] 0.211 0.158 0.082 0.491 0.078 0.060 5.0 14.0 2.60
thetas[17] 0.067 0.045 0.005 0.148 0.020 0.015 6.0 19.0 1.97
thetas[18] 0.076 0.043 0.019 0.164 0.020 0.015 5.0 13.0 2.17
thetas[19] 0.132 0.113 0.018 0.336 0.055 0.043 5.0 11.0 2.34
thetas[20] 0.121 0.079 0.029 0.260 0.038 0.030 5.0 11.0 2.20
thetas[21] 0.059 0.054 0.003 0.173 0.026 0.020 5.0 13.0 2.56
thetas[22] 0.208 0.098 0.082 0.338 0.048 0.037 5.0 19.0 2.64
thetas[23] 0.116 0.048 0.033 0.198 0.021 0.016 5.0 20.0 2.01
thetas[24] 0.121 0.065 0.029 0.232 0.031 0.024 5.0 14.0 2.62
thetas[25] 0.222 0.092 0.066 0.315 0.045 0.034 5.0 30.0 2.12
thetas[26] 0.208 0.093 0.090 0.336 0.045 0.035 5.0 15.0 2.29
thetas[27] 0.130 0.051 0.051 0.210 0.024 0.019 5.0 29.0 2.53
thetas[28] 0.122 0.033 0.034 0.160 0.008 0.006 10.0 22.0 1.44
thetas[29] 0.203 0.061 0.111 0.312 0.029 0.022 5.0 11.0 2.66
thetas[30] 0.122 0.064 0.024 0.210 0.031 0.024 5.0 12.0 3.09
thetas[31] 0.168 0.061 0.074 0.276 0.030 0.023 5.0 21.0 2.53
thetas[32] 0.112 0.040 0.046 0.189 0.018 0.014 5.0 12.0 2.33
thetas[33] 0.123 0.061 0.044 0.221 0.030 0.023 4.0 13.0 3.38
thetas[34] 0.091 0.026 0.054 0.137 0.010 0.007 8.0 28.0 1.46
thetas[35] 0.192 0.094 0.059 0.315 0.043 0.033 6.0 16.0 1.99
thetas[36] 0.121 0.069 0.021 0.267 0.025 0.018 8.0 13.0 1.47
thetas[37] 0.145 0.045 0.065 0.233 0.018 0.013 6.0 18.0 1.78
thetas[38] 0.188 0.057 0.083 0.251 0.028 0.021 6.0 16.0 2.20
thetas[39] 0.233 0.060 0.150 0.336 0.027 0.021 6.0 15.0 1.87
thetas[40] 0.169 0.085 0.049 0.323 0.041 0.031 4.0 11.0 3.16
thetas[41] 0.153 0.044 0.062 0.210 0.017 0.013 7.0 17.0 1.58
thetas[42] 0.257 0.031 0.199 0.317 0.010 0.008 10.0 12.0 1.47
thetas[43] 0.229 0.058 0.126 0.294 0.027 0.021 5.0 13.0 2.52
thetas[44] 0.305 0.086 0.193 0.410 0.042 0.032 5.0 17.0 2.79
thetas[45] 0.198 0.057 0.115 0.312 0.027 0.021 5.0 13.0 2.92
thetas[46] 0.164 0.030 0.108 0.219 0.011 0.008 8.0 17.0 1.46
thetas[47] 0.321 0.062 0.247 0.437 0.029 0.022 6.0 16.0 1.88
thetas[48] 0.278 0.058 0.161 0.346 0.027 0.021 5.0 26.0 3.02
thetas[49] 0.280 0.068 0.189 0.404 0.033 0.025 5.0 19.0 2.33
thetas[50] 0.209 0.065 0.108 0.304 0.031 0.024 5.0 13.0 2.31
thetas[51] 0.254 0.073 0.156 0.390 0.035 0.027 5.0 13.0 2.83
thetas[52] 0.233 0.072 0.124 0.337 0.034 0.026 6.0 18.0 1.89
thetas[53] 0.267 0.155 0.112 0.558 0.077 0.059 5.0 23.0 2.63
thetas[54] 0.268 0.119 0.081 0.445 0.055 0.043 5.0 14.0 2.17
thetas[55] 0.266 0.063 0.145 0.354 0.024 0.018 7.0 15.0 1.66
thetas[56] 0.249 0.035 0.192 0.316 0.014 0.011 6.0 17.0 1.67
thetas[57] 0.229 0.031 0.182 0.297 0.013 0.010 5.0 11.0 1.99
thetas[58] 0.335 0.055 0.249 0.449 0.026 0.020 5.0 11.0 2.45
thetas[59] 0.259 0.092 0.101 0.416 0.041 0.031 5.0 15.0 2.02
thetas[60] 0.312 0.106 0.134 0.436 0.051 0.040 5.0 13.0 3.03
thetas[61] 0.247 0.063 0.141 0.371 0.028 0.021 5.0 11.0 2.15
thetas[62] 0.356 0.135 0.194 0.545 0.066 0.051 4.0 14.0 3.28
thetas[63] 0.362 0.087 0.232 0.501 0.042 0.032 5.0 13.0 2.74
thetas[64] 0.298 0.097 0.122 0.452 0.045 0.035 5.0 12.0 2.51
thetas[65] 0.324 0.099 0.222 0.486 0.048 0.037 5.0 15.0 2.28
thetas[66] 0.306 0.079 0.172 0.401 0.038 0.029 5.0 11.0 2.54
thetas[67] 0.348 0.090 0.224 0.462 0.045 0.034 4.0 11.0 3.99
thetas[68] 0.320 0.038 0.272 0.390 0.017 0.013 5.0 23.0 2.21
thetas[69] 0.403 0.053 0.266 0.471 0.019 0.014 10.0 11.0 1.54
thetas[70] 0.383 0.126 0.202 0.601 0.062 0.048 4.0 11.0 3.20

r_hat is showing measure of each chain is converged to stationary distribution. r_hat should be less than or equal to 1.01, here we get r_hat far from 1.01 for each latent sample.

Hide code cell source 
az.plot_trace(trace)
plt.tight_layout();
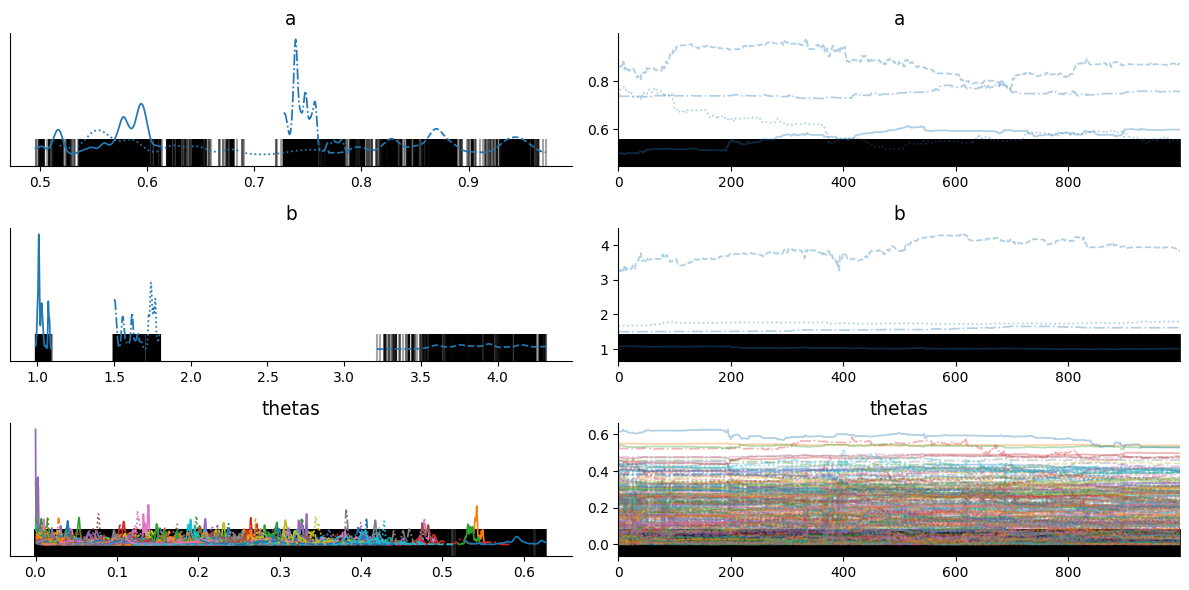
../_images/116e3c16e8b3583966ca19e7c8f26096da05dafb60db91535ac9b44676dbac62.png

Trace plots also looks terrible and does not seems to be converged! Also, black band shows that every sample is diverged from original distribution. So what’s wrong happeing here?

Well, it’s related to support of latent variable. In HMC, the latent variable must be in an unconstrained space, but in above model theta is constrained in between 0 to 1. We can use change of variable trick to solve above problem

Change of Variable#

We can sample from logits which is in unconstrained space and in joint_logdensity() we can convert logits to theta by suitable bijector (sigmoid). We calculate jacobian (first order derivaive) of bijector to tranform one probability distribution to another

transform_fn = jax.nn.sigmoid
log_jacobian_fn = lambda logit: jnp.log(jnp.abs(jnp.diag(jax.jacfwd(transform_fn)(logit))))

Alternatively, using the bijector class in TFP directly:

bij = tfb.Sigmoid()
transform_fn = bij.forward
log_jacobian_fn = bij.forward_log_det_jacobian

params = namedtuple("model_params", ["a", "b", "logits"])

def joint_logdensity_change_of_var(params):
    # change of variable
    thetas = transform_fn(params.logits)
    log_det_jacob = jnp.sum(log_jacobian_fn(params.logits))

    # improper prior for a,b
    logdensity_ab = jnp.log(jnp.power(params.a + params.b, -2.5))

    # logdensity prior of theta
    logdensity_thetas = tfd.Beta(params.a, params.b).log_prob(thetas).sum()

    # loglikelihood of y
    logdensity_y = jnp.sum(
        tfd.Binomial(group_size, probs=thetas).log_prob(n_of_positives)
    )

    return logdensity_ab + logdensity_thetas + logdensity_y + log_det_jacob

except for the change of variable in joint_logdensity() function, everthing will remain same

rng_key, init_key = jax.random.split(rng_key)


def init_param_fn(seed):
    """
    initialize a, b & logits
    """
    key1, key2, key3 = jax.random.split(seed, 3)
    return params(
        a=tfd.Uniform(0, 3).sample(seed=key1),
        b=tfd.Uniform(0, 3).sample(seed=key2),
        logits=tfd.Uniform(-2, 2).sample(n_rat_tumors, key3),
    )


init_param = init_param_fn(init_key)
joint_logdensity_change_of_var(init_param)  # sanity check

Array(-1093.7466, dtype=float32)

%%time
warmup = blackjax.window_adaptation(blackjax.nuts, joint_logdensity_change_of_var)

# we use 4 chains for sampling
n_chains = 4
rng_key, init_key, warmup_key = jax.random.split(rng_key, 3)
init_keys = jax.random.split(init_key, n_chains)
init_params = jax.vmap(init_param_fn)(init_keys)

@jax.vmap
def call_warmup(seed, param):
    (initial_states, tuned_params), _ = warmup.run(seed, param, 1000)
    return initial_states, tuned_params

warmup_keys = jax.random.split(warmup_key, n_chains)
initial_states, tuned_params = call_warmup(warmup_keys, init_params)

CPU times: user 8.27 s, sys: 451 ms, total: 8.72 s
Wall time: 5.98 s

%%time
n_samples = 1000
rng_key, sample_key = jax.random.split(rng_key)
states, infos = inference_loop_multiple_chains(
    sample_key, initial_states, tuned_params, joint_logdensity_change_of_var, n_samples, n_chains
)

CPU times: user 6.62 s, sys: 522 ms, total: 7.14 s
Wall time: 3.08 s

# convert logits samples to theta samples
position = states.position._asdict()
position["thetas"] = jax.nn.sigmoid(position["logits"])
del position["logits"]  # delete logits
states = states._replace(position=position)

# make arviz trace from states
trace = arviz_trace_from_states(states, infos, burn_in=0)
summ_df = az.summary(trace)
summ_df
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
a 2.383 0.848 1.106 4.013 0.035 0.026 689.0 930.0 1.01
b 14.218 5.131 6.206 23.643 0.200 0.153 761.0 1105.0 1.01
thetas[0] 0.063 0.040 0.000 0.133 0.001 0.000 3795.0 2436.0 1.00
thetas[1] 0.063 0.042 0.001 0.138 0.001 0.000 3114.0 1986.0 1.00
thetas[2] 0.063 0.040 0.001 0.134 0.001 0.000 3433.0 2150.0 1.00
thetas[3] 0.062 0.042 0.001 0.135 0.001 0.000 3562.0 2298.0 1.00
thetas[4] 0.062 0.040 0.001 0.135 0.001 0.000 3098.0 2037.0 1.00
thetas[5] 0.063 0.040 0.003 0.134 0.001 0.000 3339.0 2131.0 1.00
thetas[6] 0.064 0.042 0.001 0.140 0.001 0.000 3995.0 1836.0 1.00
thetas[7] 0.065 0.042 0.003 0.140 0.001 0.000 3626.0 2138.0 1.00
thetas[8] 0.064 0.041 0.003 0.137 0.001 0.000 3660.0 2087.0 1.00
thetas[9] 0.065 0.042 0.003 0.143 0.001 0.000 3633.0 1747.0 1.00
thetas[10] 0.064 0.042 0.000 0.140 0.001 0.000 3114.0 1997.0 1.00
thetas[11] 0.067 0.045 0.000 0.149 0.001 0.001 3174.0 1897.0 1.00
thetas[12] 0.068 0.045 0.001 0.148 0.001 0.000 3708.0 2177.0 1.00
thetas[13] 0.069 0.044 0.002 0.149 0.001 0.000 3111.0 1430.0 1.00
thetas[14] 0.092 0.050 0.009 0.180 0.001 0.000 5622.0 2337.0 1.00
thetas[15] 0.092 0.050 0.009 0.183 0.001 0.001 5502.0 2693.0 1.00
thetas[16] 0.091 0.050 0.011 0.178 0.001 0.000 6980.0 2297.0 1.00
thetas[17] 0.091 0.048 0.012 0.178 0.001 0.000 6260.0 1925.0 1.00
thetas[18] 0.093 0.050 0.013 0.186 0.001 0.000 5904.0 2533.0 1.00
thetas[19] 0.094 0.049 0.014 0.187 0.001 0.000 6018.0 2372.0 1.00
thetas[20] 0.096 0.049 0.017 0.186 0.001 0.000 6021.0 2598.0 1.00
thetas[21] 0.097 0.052 0.011 0.193 0.001 0.001 6441.0 2208.0 1.00
thetas[22] 0.105 0.049 0.023 0.193 0.001 0.000 7076.0 2039.0 1.00
thetas[23] 0.107 0.049 0.023 0.198 0.001 0.000 6212.0 2437.0 1.00
thetas[24] 0.110 0.050 0.030 0.211 0.001 0.001 6929.0 2640.0 1.00
thetas[25] 0.120 0.052 0.028 0.220 0.001 0.000 6661.0 2774.0 1.00
thetas[26] 0.120 0.053 0.027 0.216 0.001 0.001 7717.0 3076.0 1.00
thetas[27] 0.120 0.053 0.026 0.214 0.001 0.000 7034.0 2235.0 1.00
thetas[28] 0.119 0.054 0.026 0.217 0.001 0.000 7774.0 2420.0 1.00
thetas[29] 0.121 0.056 0.025 0.222 0.001 0.001 6871.0 2518.0 1.00
thetas[30] 0.120 0.054 0.026 0.218 0.001 0.000 8127.0 2559.0 1.00
thetas[31] 0.127 0.065 0.015 0.239 0.001 0.001 7381.0 2664.0 1.00
thetas[32] 0.112 0.039 0.046 0.188 0.000 0.000 8782.0 2797.0 1.00
thetas[33] 0.124 0.055 0.031 0.226 0.001 0.001 7425.0 2606.0 1.00
thetas[34] 0.117 0.041 0.049 0.197 0.000 0.000 7939.0 2322.0 1.00
thetas[35] 0.124 0.050 0.039 0.220 0.001 0.000 7691.0 2820.0 1.00
thetas[36] 0.130 0.057 0.032 0.235 0.001 0.000 7815.0 2685.0 1.00
thetas[37] 0.143 0.042 0.064 0.221 0.001 0.000 6609.0 2485.0 1.00
thetas[38] 0.148 0.045 0.066 0.229 0.000 0.000 9453.0 2779.0 1.00
thetas[39] 0.147 0.059 0.045 0.255 0.001 0.001 8074.0 2241.0 1.00
thetas[40] 0.147 0.059 0.038 0.252 0.001 0.001 8127.0 2658.0 1.00
thetas[41] 0.149 0.065 0.042 0.277 0.001 0.001 8606.0 2641.0 1.00
thetas[42] 0.176 0.048 0.092 0.266 0.001 0.000 9224.0 2204.0 1.00
thetas[43] 0.187 0.048 0.101 0.281 0.000 0.000 9276.0 2630.0 1.00
thetas[44] 0.175 0.064 0.068 0.297 0.001 0.001 9094.0 2636.0 1.00
thetas[45] 0.175 0.062 0.070 0.290 0.001 0.001 9291.0 2738.0 1.00
thetas[46] 0.176 0.064 0.060 0.295 0.001 0.001 8498.0 2734.0 1.00
thetas[47] 0.175 0.063 0.065 0.292 0.001 0.001 7688.0 2373.0 1.00
thetas[48] 0.175 0.063 0.065 0.296 0.001 0.001 8067.0 2836.0 1.00
thetas[49] 0.175 0.063 0.065 0.297 0.001 0.001 9197.0 2345.0 1.00
thetas[50] 0.174 0.062 0.064 0.287 0.001 0.001 7198.0 2795.0 1.00
thetas[51] 0.192 0.050 0.103 0.285 0.000 0.000 9522.0 2558.0 1.00
thetas[52] 0.181 0.066 0.071 0.308 0.001 0.001 8427.0 2617.0 1.00
thetas[53] 0.179 0.063 0.062 0.293 0.001 0.001 7779.0 2789.0 1.00
thetas[54] 0.180 0.064 0.067 0.295 0.001 0.001 7060.0 2746.0 1.00
thetas[55] 0.193 0.064 0.081 0.314 0.001 0.001 7438.0 2858.0 1.00
thetas[56] 0.214 0.052 0.121 0.312 0.001 0.000 7345.0 2891.0 1.00
thetas[57] 0.220 0.052 0.127 0.316 0.001 0.000 6789.0 2858.0 1.00
thetas[58] 0.202 0.069 0.079 0.330 0.001 0.001 7473.0 3055.0 1.00
thetas[59] 0.203 0.065 0.088 0.326 0.001 0.001 7758.0 2908.0 1.00
thetas[60] 0.214 0.065 0.098 0.340 0.001 0.001 6202.0 2682.0 1.00
thetas[61] 0.209 0.071 0.085 0.341 0.001 0.001 7723.0 2565.0 1.00
thetas[62] 0.218 0.068 0.097 0.344 0.001 0.001 7942.0 2535.0 1.00
thetas[63] 0.232 0.071 0.101 0.363 0.001 0.001 5444.0 2739.0 1.00
thetas[64] 0.231 0.071 0.104 0.358 0.001 0.001 9137.0 2559.0 1.00
thetas[65] 0.231 0.072 0.104 0.363 0.001 0.001 6290.0 2399.0 1.00
thetas[66] 0.270 0.054 0.178 0.373 0.001 0.000 7124.0 2905.0 1.00
thetas[67] 0.279 0.056 0.177 0.384 0.001 0.001 5907.0 3276.0 1.00
thetas[68] 0.275 0.058 0.168 0.386 0.001 0.001 6059.0 2381.0 1.00
thetas[69] 0.283 0.072 0.149 0.416 0.001 0.001 5234.0 2415.0 1.00
thetas[70] 0.211 0.075 0.082 0.356 0.001 0.001 8011.0 2775.0 1.00
Hide code cell source 
az.plot_trace(trace)
plt.tight_layout();
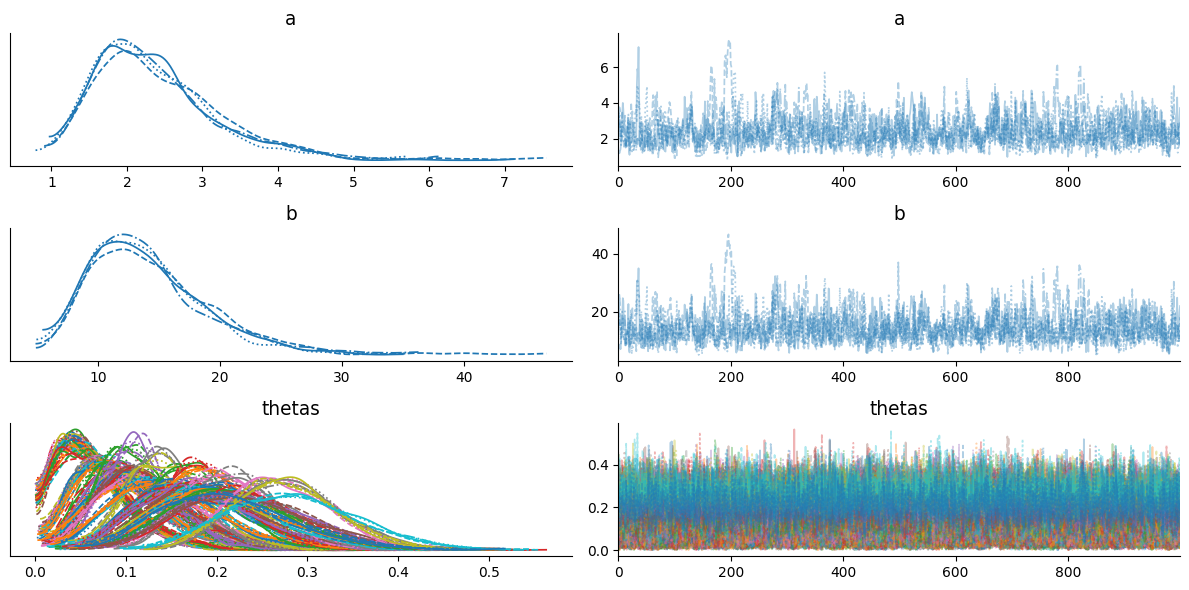
../_images/0b3a8b99595dae7e7f11d2d12b1cb36541e0a4eff9331878f5c62a57c7745b10.png 
print(f"Number of divergence: {infos.is_divergent.sum()}")

Number of divergence: 0

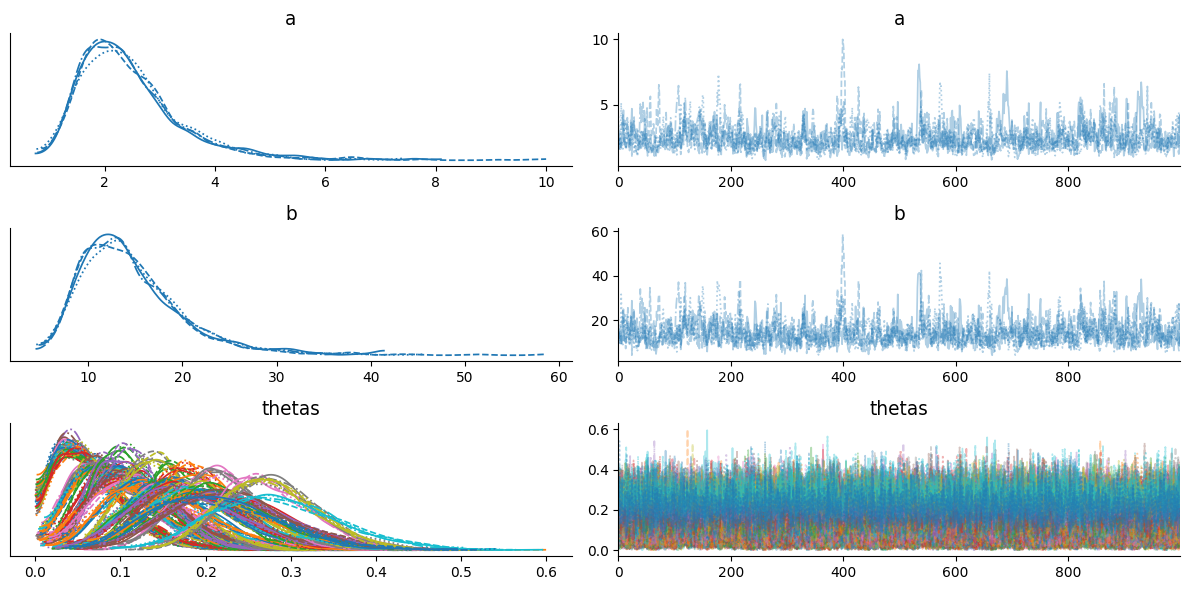
We can see that r_hat is less than or equal to 1.01 for each latent variable, trace plots looks converged to stationary distribution, and only few samples are diverged.

Using a PPL#

Probabilistic programming language usually provides functionality to apply change of variable easily (often done automatically). In this case for TFP, we can use its modeling API tfd.JointDistribution*.

tfed = tfp.experimental.distributions

@tfd.JointDistributionCoroutineAutoBatched
def model():
    # TFP does not have improper prior, use uninformative prior instead
    a = yield tfd.HalfCauchy(0, 100, name='a')
    b = yield tfd.HalfCauchy(0, 100, name='b')
    yield tfed.IncrementLogProb(jnp.log(jnp.power(a + b, -2.5)), name='logdensity_ab')

    thetas = yield tfd.Sample(tfd.Beta(a, b), n_rat_tumors, name='thetas')
    yield tfd.Binomial(group_size, probs=thetas, name='y')

# Sample from the prior and prior predictive distributions. The result is a pytree.
# model.sample(seed=rng_key)

# Condition on the observed (and auxiliary variable).
pinned = model.experimental_pin(logdensity_ab=(), y=n_of_positives)
# Get the default change of variable bijectors from the model
bijectors = pinned.experimental_default_event_space_bijector()

rng_key, init_key = jax.random.split(rng_key)
prior_sample = pinned.sample_unpinned(seed=init_key)
# You can check the unbounded sample
# bijectors.inverse(prior_sample)

def joint_logdensity(unbound_param):
    param = bijectors.forward(unbound_param)
    log_det_jacobian = bijectors.forward_log_det_jacobian(unbound_param)
    return pinned.unnormalized_log_prob(param) + log_det_jacobian

%%time
warmup = blackjax.window_adaptation(blackjax.nuts, joint_logdensity)

# we use 4 chains for sampling
n_chains = 4
rng_key, init_key, warmup_key = jax.random.split(rng_key, 3)
init_params = bijectors.inverse(pinned.sample_unpinned(n_chains, seed=init_key))

@jax.vmap
def call_warmup(seed, param):
    (initial_states, tuned_params), _ = warmup.run(seed, param, 1000)
    return initial_states, tuned_params

warmup_keys = jax.random.split(warmup_key, n_chains)
initial_states, tuned_params = call_warmup(warmup_keys, init_params)

CPU times: user 10.7 s, sys: 599 ms, total: 11.3 s
Wall time: 7.06 s

%%time
n_samples = 1000
rng_key, sample_key = jax.random.split(rng_key)
states, infos = inference_loop_multiple_chains(
    sample_key, initial_states, tuned_params, joint_logdensity, n_samples, n_chains
)

CPU times: user 7.53 s, sys: 551 ms, total: 8.08 s
Wall time: 3.87 s

# convert logits samples to theta samples
position = states.position
states = states._replace(position=bijectors.forward(position))

# make arviz trace from states
trace = arviz_trace_from_states(states, infos, burn_in=0)
summ_df = az.summary(trace)
summ_df
mean sd hdi_3% hdi_97% mcse_mean mcse_sd ess_bulk ess_tail r_hat
a 2.448 0.954 1.071 4.237 0.037 0.026 673.0 1112.0 1.01
b 14.572 5.602 5.741 24.480 0.210 0.149 740.0 1171.0 1.01
thetas[0] 0.064 0.042 0.001 0.138 0.001 0.001 2577.0 1921.0 1.00
thetas[1] 0.064 0.043 0.001 0.144 0.001 0.000 2757.0 1474.0 1.00
thetas[2] 0.063 0.041 0.001 0.134 0.001 0.000 2721.0 1752.0 1.00
thetas[3] 0.065 0.042 0.001 0.137 0.001 0.000 2850.0 1886.0 1.00
thetas[4] 0.065 0.042 0.001 0.141 0.001 0.000 2987.0 1934.0 1.00
thetas[5] 0.064 0.042 0.000 0.136 0.001 0.000 2844.0 1695.0 1.00
thetas[6] 0.064 0.041 0.002 0.139 0.001 0.001 2498.0 2113.0 1.00
thetas[7] 0.066 0.043 0.001 0.143 0.001 0.000 2875.0 1646.0 1.00
thetas[8] 0.066 0.042 0.002 0.143 0.001 0.001 2667.0 1926.0 1.00
thetas[9] 0.066 0.043 0.000 0.144 0.001 0.001 2826.0 2372.0 1.00
thetas[10] 0.066 0.044 0.002 0.146 0.001 0.001 3598.0 2342.0 1.00
thetas[11] 0.069 0.044 0.000 0.147 0.001 0.001 3027.0 2127.0 1.00
thetas[12] 0.068 0.044 0.000 0.146 0.001 0.001 2895.0 1746.0 1.00
thetas[13] 0.070 0.046 0.000 0.150 0.001 0.001 2942.0 1929.0 1.00
thetas[14] 0.092 0.049 0.009 0.180 0.001 0.001 4120.0 2216.0 1.00
thetas[15] 0.091 0.047 0.016 0.178 0.001 0.001 3927.0 2050.0 1.00
thetas[16] 0.092 0.049 0.014 0.184 0.001 0.001 5132.0 2243.0 1.00
thetas[17] 0.092 0.048 0.012 0.180 0.001 0.001 3820.0 2346.0 1.00
thetas[18] 0.096 0.051 0.014 0.192 0.001 0.001 4867.0 2265.0 1.00
thetas[19] 0.095 0.051 0.011 0.186 0.001 0.001 4954.0 2603.0 1.00
thetas[20] 0.096 0.050 0.012 0.190 0.001 0.000 4375.0 2077.0 1.00
thetas[21] 0.098 0.051 0.016 0.191 0.001 0.001 5533.0 2158.0 1.00
thetas[22] 0.105 0.049 0.022 0.192 0.001 0.000 5694.0 2210.0 1.00
thetas[23] 0.108 0.048 0.029 0.199 0.001 0.000 5515.0 2660.0 1.00
thetas[24] 0.111 0.048 0.023 0.194 0.001 0.000 5517.0 2563.0 1.00
thetas[25] 0.119 0.053 0.035 0.222 0.001 0.001 4961.0 2276.0 1.00
thetas[26] 0.118 0.053 0.027 0.215 0.001 0.000 5456.0 2690.0 1.00
thetas[27] 0.119 0.054 0.033 0.222 0.001 0.001 6172.0 2737.0 1.00
thetas[28] 0.119 0.053 0.026 0.220 0.001 0.001 5452.0 2360.0 1.00
thetas[29] 0.120 0.052 0.033 0.218 0.001 0.000 6322.0 2644.0 1.00
thetas[30] 0.120 0.054 0.030 0.218 0.001 0.001 6348.0 2713.0 1.00
thetas[31] 0.128 0.064 0.025 0.248 0.001 0.001 6615.0 2569.0 1.00
thetas[32] 0.113 0.040 0.044 0.190 0.000 0.000 6631.0 2725.0 1.00
thetas[33] 0.123 0.054 0.034 0.227 0.001 0.001 5944.0 2311.0 1.00
thetas[34] 0.117 0.041 0.045 0.192 0.001 0.000 5906.0 2884.0 1.00
thetas[35] 0.123 0.051 0.037 0.220 0.001 0.000 6259.0 2736.0 1.00
thetas[36] 0.130 0.057 0.030 0.233 0.001 0.001 5933.0 2565.0 1.00
thetas[37] 0.144 0.042 0.069 0.220 0.001 0.000 6879.0 2959.0 1.00
thetas[38] 0.147 0.045 0.065 0.229 0.001 0.000 6195.0 2517.0 1.00
thetas[39] 0.146 0.057 0.050 0.255 0.001 0.001 5635.0 2575.0 1.00
thetas[40] 0.148 0.059 0.048 0.257 0.001 0.001 6105.0 2262.0 1.00
thetas[41] 0.148 0.065 0.035 0.270 0.001 0.001 6234.0 2539.0 1.00
thetas[42] 0.176 0.048 0.091 0.267 0.001 0.000 6150.0 2698.0 1.00
thetas[43] 0.185 0.049 0.101 0.279 0.001 0.000 6072.0 2927.0 1.00
thetas[44] 0.174 0.062 0.062 0.287 0.001 0.001 7229.0 2940.0 1.00
thetas[45] 0.175 0.062 0.071 0.300 0.001 0.001 5886.0 2538.0 1.00
thetas[46] 0.175 0.061 0.068 0.289 0.001 0.001 6640.0 2702.0 1.00
thetas[47] 0.176 0.063 0.063 0.293 0.001 0.001 7861.0 2910.0 1.00
thetas[48] 0.174 0.063 0.063 0.291 0.001 0.001 6447.0 2645.0 1.00
thetas[49] 0.175 0.063 0.063 0.290 0.001 0.001 6677.0 3001.0 1.00
thetas[50] 0.176 0.060 0.068 0.288 0.001 0.001 6059.0 2792.0 1.00
thetas[51] 0.192 0.049 0.109 0.292 0.001 0.000 6417.0 2835.0 1.00
thetas[52] 0.180 0.064 0.069 0.297 0.001 0.001 5411.0 2596.0 1.00
thetas[53] 0.181 0.064 0.073 0.310 0.001 0.001 5868.0 2458.0 1.00
thetas[54] 0.182 0.066 0.059 0.295 0.001 0.001 6763.0 2608.0 1.00
thetas[55] 0.193 0.064 0.084 0.319 0.001 0.001 6305.0 2502.0 1.00
thetas[56] 0.214 0.051 0.126 0.315 0.001 0.001 5463.0 2389.0 1.00
thetas[57] 0.219 0.051 0.127 0.315 0.001 0.000 5525.0 2489.0 1.00
thetas[58] 0.203 0.067 0.087 0.333 0.001 0.001 6904.0 2739.0 1.00
thetas[59] 0.204 0.068 0.081 0.327 0.001 0.001 4985.0 2483.0 1.00
thetas[60] 0.214 0.067 0.098 0.341 0.001 0.001 6661.0 2901.0 1.00
thetas[61] 0.210 0.071 0.074 0.332 0.001 0.001 5737.0 2461.0 1.00
thetas[62] 0.217 0.068 0.098 0.351 0.001 0.001 5632.0 2385.0 1.00
thetas[63] 0.231 0.073 0.095 0.361 0.001 0.001 5032.0 2817.0 1.00
thetas[64] 0.231 0.073 0.099 0.368 0.001 0.001 5379.0 2664.0 1.00
thetas[65] 0.230 0.071 0.107 0.366 0.001 0.001 5864.0 2938.0 1.00
thetas[66] 0.268 0.056 0.164 0.377 0.001 0.001 4504.0 2034.0 1.00
thetas[67] 0.277 0.057 0.174 0.391 0.001 0.001 4531.0 3003.0 1.00
thetas[68] 0.274 0.055 0.169 0.372 0.001 0.001 5178.0 3218.0 1.00
thetas[69] 0.282 0.074 0.148 0.426 0.001 0.001 4129.0 2787.0 1.00
thetas[70] 0.211 0.075 0.083 0.351 0.001 0.001 6038.0 2857.0 1.00
Hide code cell source 
az.plot_trace(trace)
plt.tight_layout();
../_images/4555c18fbd04152a81a80dcc51405429527989d93347c6be946b61d989260633.png
Contents